yukicoder No.737 PopCount

問題

V(x) = x * popcount(x) とするとき、 \displaystyle \sum_{i=1}^{N} V(i) を求めよ。

制約

n(1 \le n \le 10^{18})

考え方

まず数を 2 進数の桁ごとに分けて考える。

たとえば 3(10) = 0011(2) で V(3) = 3 * popcount(3) = 3 * 2 = 6 であるが、これは 0 ビット目と 1 ビット目で 1 のそれぞれで 3 を足せばよい。

さて、求めたいのは

f(n, k) := n までの数で k ビット目が 1 である数の総和

として、 \displaystyle \sum_{k=1}^{63} f(n, k) である。f(n, k) の求め方について考えていこう。

例として f(30, 1) について考える。 0 から 30 の数のうち 1 ビット目が 1 になっている数を列挙すると

2,3,6,7,10,11,14,15,18,19,22,23,26,27 の 15 つの数である。これは初項が 2, 3 で公差が 2^2 となっている等差数列として考えることができる。しかしそう考えると k ビット目の場合は、初項 2^k+m (0 \le m \le 2^{k-1}) で公差 2^{k+1} の等差数列のそれぞれの和について求める必要があり、この計算量は O(2^{k}) であるから求めることはできない。もう少し等差数列の和をまとめて計算する必要がある。

以下の図からわかるように n までの数のうち、 k ビット目に含まれる 0,1 の数には分布には規則性がある。例えば 1 ビット目は 0 から 0,0,1,1 というパターンがあり、このパターンが 30 までに 7 つ含まれている事がわかる。また、 30 のうち、パターンに含まれない数も高速に求めることができる。0 から考えて、長さ 4 のパターンは 7 つあるから残りの数は [4*7, 30] である。このうち、最初の 2^1 個目までの数の 1 ビット目は 0 になっていて、残りの数が 1 となっている。

パターンに含まれる数の和は、パターンごとの総和を考えると 1 ビット目の場合、5,13,21,29,37,45,53 となっていることがわかる。これは初項 5 で公差が 2^3 項数 7 の等差数列の和をとることで O(1) で求めることができる。

パターンに含まれない数の和は初項 30 公差 1 で末項 30 の等差数列の和を求めれば良い。

f:id:d_tutuz:20180929124603p:plain

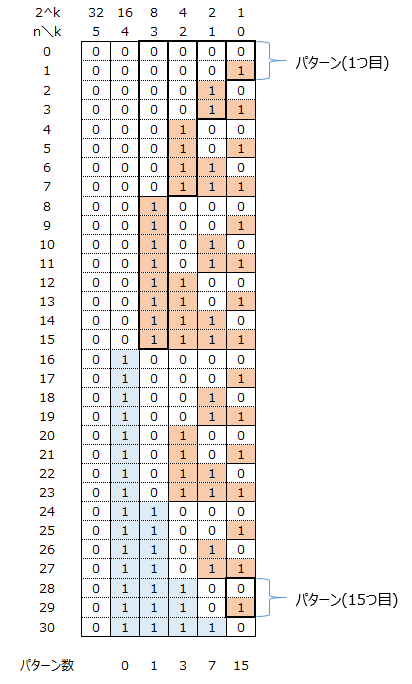
上記の内容を一般化すると、

n までの数のうち k ビット目は・・・

  • パターンが \displaystyle \frac{n+1}{2 * 2^k} 個
  • パターンに含まれる数の総和は初項が 「初項 2^k 公差 1 項数 k の等差数列の和」、公差が 2^{2*k+1} 項数 \displaystyle \frac{n+1}{2 * 2^k} の等差数列の和（＝上の図でいうところのオレンジ背景の部分）
  • パターンに含まれない数の総和は 初項 \displaystyle \frac{n+1}{2 * 2^k} * (2 * 2^k) + 2^k 公差 1 項数 (n+1) \% (2 * 2^k) - 2^k の等差数列の和 （＝上の図でいうところの水色背景の部分）

となっている。

       public void solve(int testNumber, InputReader in, PrintWriter out) {

            long n = in.nextLong();

            long ans = 0;
            for (long k = 1; k <= n; k <<= 1) {
                long sum = sum(k, 1, k);
                long len = (n+1) / (2*k);
                ans += sum(sum, k % MOD * (2 * k % MOD) % MOD, len);
                ans %= MOD;
                long to = (n+1) % (2*k) - k;
                if (to > 0) {
                    long from = (n+1) / (2*k) * (2*k) + k;
                    ans += sum(from, 1, to);
                    ans %= MOD;
                }
            }

            out.println(ans);

        }

        long sum(long a, long d, long n) {
            a %= MOD;
            d %= MOD;
            n %= MOD;
            return n * (2 * a % MOD + (n + MOD - 1) % MOD * d % MOD) % MOD * INV2 % MOD;
        }

ポイント

パターンごとにまとめて考える

類題

雑記

本番中は popcount(x) の数が同じものでまとめられれば、同じ popcount(x) の数はまとめて計算できるのでは・・・。と考えていたが、popcount(x) の数が同じものでまとめれることを高速に実施することは難しそうと判断して、解けないなぁ...と思っていた。