問題

縦 r 、横 c の r × c のグリッドがあたえられる。グリッドのマスは * か . で構成される。.のマスに広告を打つが上下左右に隣り合うように広告は打てない。広告を打つ最大数を求めよ。

考え方

グリッドグラフ上で考える。上下左右に隣り合う頂点に広告を打つことができないため、広告を打つことのできる頂点の集合は安定集合になっている。よって求める解はグリッドグラフ上の最大安定集合のサイズということになる。

グリッドグラフ上の最大安定集合を求めることについて考える。グリッドグラフの各頂点は上下左右の4マスにしか辺が存在しない。頂点 (i, j) について、i + j が偶数の場合と奇数の場合に分けて市松模様のようになっているグラフと考えると、このグリッドグラフは二部グラフになっている。

サンプル4のケースでは以下のような二部グラフになっていると考えることができる。 ※丸の中が塗りつぶされている頂点は*のため遷移できない。

f:id:d_tutuz:20180815213253p:plain

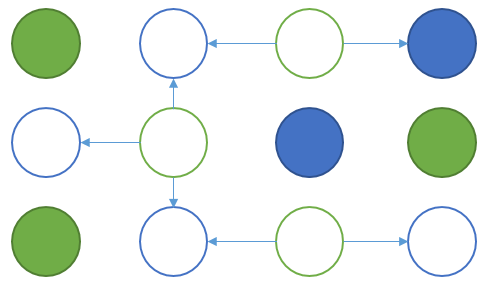
二部グラフの最大安定集合のサイズは、「頂点数 - 最大マッチングサイズ」で求められる。よって後は二部グラフの最大マッチングサイズを求めればよいが、これは、Dinic法などのアルゴリズムによって求められる。