AGC009-B：Tournament

問題

https://beta.atcoder.jp/contests/agc009/tasks/agc009_b

考え方

木DPだが、遷移が重要。今ある親 u から 4 個の子 (v_1, v_2, v_3, v_4)をもつ部分木の場合を考える。ある頂点の深さを cost[p] としておく。

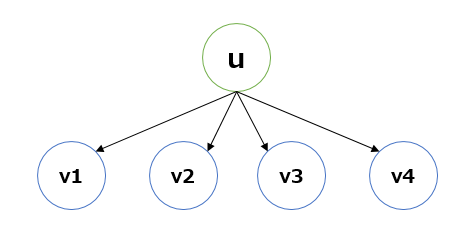
このとき、トーナメントの割当としては以下のようになる。

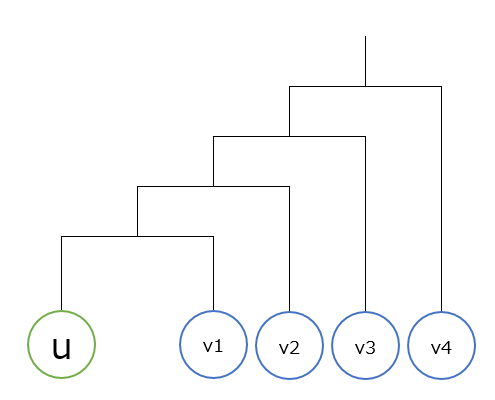
u は v_1, v_2, v_3, v_4 のいずれとも試合をするが、このとき u の深さが最適に(一番浅く)なるときは、深い場所に一番浅い頂点をもつように、すなわち cost[v_1] >= cost[v_2] >= cost[v_3] >= cost[v_4] となるように割り当てるのが最適である。

このとき u の深さ cost[u] は cost[v_k] を降順にソートしておいて cost[u] = cost[v_k] + k+1 となる

       List<Integer>[] g;
        public void solve(int testNumber, InputReader in, PrintWriter out) {

            int n = in.nextInt();
            g = new ArrayList[n];
            g = Stream.generate(ArrayList::new).limit(n).toArray(List[]::new);

            for (int i = 1; i < n; i++) {
                int a = in.nextInt()-1;
                g[a].add(i);
            }
            int ans = dfs(0);
            out.println(ans);

        }

        int dfs(int now) {

            List<Integer> list = new ArrayList<>();
            for (int next : g[now]) {
                list.add(dfs(next));
            }
            Collections.sort(list, Comparator.reverseOrder());
            int ret = 0;
            for (int i = 0; i < list.size(); i++) {
                ret = Math.max(ret, i+1 + list.get(i));
            }

            return ret;
        }

ポイント

• 実験して遷移を考える

類題