問題

https://beta.atcoder.jp/contests/abc111/tasks/arc103_b

制約

$1 \le N \le 1000$
$|X_i|,\ |Y_i| \le 10^9$

考え方

必要条件を考える

まず、構成するための必要条件を考える。 $m$ つの腕を定めたときに $n$ つの点が同時に到達できないといけない。これはそれぞれの点の距離 $x_i + y_i$ についてその偶奇が一致していないといけない。偶奇が一致していれば、十分な数の距離 $1$ の腕を使えば構成できることはわかる。

構成方法を考える

原点から $(x_i,\ y_i)$ に到達するように $d_i$ を定めないといけない。使える腕の数が $1 \le m \le 40$ と小さいので工夫して構成する必要がある。

「任意の数を作る」ときに $2$ 冪で構成することはよく知られている。 $1,2,4,\cdots,2^{30}$ の腕を使って $x_i$ を作ることができる。

さて、難しいのは $x_i, y_i$ を同時に到達するようにモードを定めることである。これは実は座標を $45$ 度変換することで解決できる。

$u = x + y$
$y = x - y$

f:id:d_tutuz:20181209220107p:plain

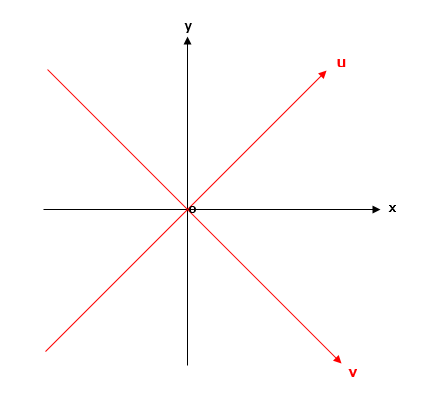
として $u-v$ 座標で考えることとすると、モードによる操作は以下のように変換されることがわかる。

	$x$	$y$		$u$	$v$
$L$	$-$	$0$	$\to$	$-$	$-$
$R$	$+$	$0$	$\to$	$+$	$+$
$U$	$0$	$+$	$\to$	$+$	$-$
$D$	$0$	$-$	$\to$	$-$	$+$

変換された後の操作は、ある操作で $uv$ のそれぞれについて同時に座標を加減することができる。そうすると後は、 $2$ 冪で構成された腕の長さの長い腕( $d=2^{30}$ )から貪欲に当てはまるモードを設定すれば良い。なお $(x_i, y_i)$ から原点への移動方法を考えるがモードの設定は移動の方向と逆向きのモードを設定する。