2018-09-30

ARC103-E:Tr/ee(700)

グラフ構築

問題

長さ n の文字列 s が与えられる。以下の条件を満たす n 頂点の木を構築することができるかどうか。

頂点 s_i の文字が 1 であれば、木から辺を 1 つ取り除いて、長さ i の連結成分を作ることができる
頂点 s_i の文字が 0 であれば、木から辺を 1 つ取り除いて、長さ i の連結成分を作ることができない

※ i は 1-indexed

考え方

まず、木を構築するための必要条件を整理する。以下の条件を満たす場合は目的の木を構築することはできない。

$s_n$ が $1$ (サイズ $n$ の木は作ることはできない)
$s_1$ が $0$ ( $1$ 本切ることで必ずサイズ $1$ の木は作るカットが存在する)
$s_i \neq s_{n - i}$ (あるカットでサイズ $i$ の連結成分を作るとき、もう片方のサイズは $n - i$ になっているため)

逆に上記の条件を満たさなければ、目的の木を構築することができる。放送解説の通りだが、以下がその一例の木である。

f:id:d_tutuz:20180930085454p:plain

ポイント

必要条件で絞り込む
対になる条件を考える

類題

2018-09-29

yukicoder No.737 PopCount

問題

$V(x) = x * popcount(x)$ とするとき、 $\displaystyle \sum_{i=1}^{N} V(i)$ を求めよ。

制約

$n(1 \le n \le 10^{18})$

考え方

まず数を $2$ 進数の桁ごとに分けて考える。

たとえば $3(10) = 0011(2)$ で $V(3) = 3 * popcount(3) = 3 * 2 = 6$ であるが、これは $0$ ビット目と $1$ ビット目で $1$ のそれぞれで $3$ を足せばよい。

さて、求めたいのは

$f(n, k)$ := n までの数で $k$ ビット目が $1$ である数の総和

として、 $\displaystyle \sum_{k=1}^{63} f(n, k)$ である。 $f(n, k)$ の求め方について考えていこう。

例として $f(30, 1)$ について考える。 $0$ から $30$ の数のうち $1$ ビット目が $1$ になっている数を列挙すると

$2,3,6,7,10,11,14,15,18,19,22,23,26,27$ の $15$ つの数である。これは初項が $2, 3$ で公差が $2^2$ となっている等差数列として考えることができる。しかしそう考えると $k$ ビット目の場合は、初項 $2^k+m (0 \le m \le 2^{k-1})$ で公差 $2^{k+1}$ の等差数列のそれぞれの和について求める必要があり、この計算量は $O(2^{k})$ であるから求めることはできない。もう少し等差数列の和をまとめて計算する必要がある。

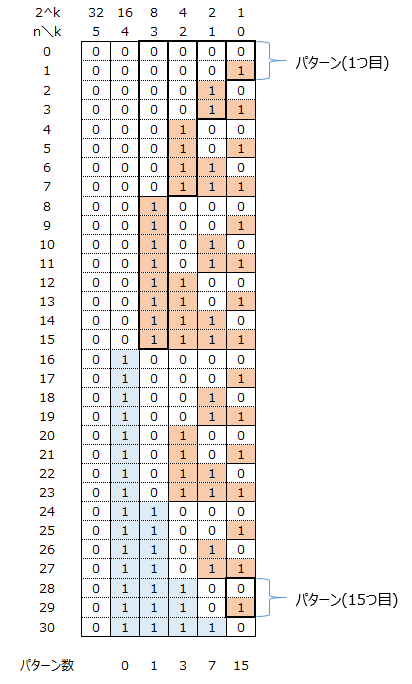
以下の図からわかるように $n$ までの数のうち、 $k$ ビット目に含まれる $0,1$ の数には分布には規則性がある。例えば $1$ ビット目は $0$ から $0,0,1,1$ というパターンがあり、このパターンが $30$ までに $7$ つ含まれている事がわかる。また、 $30$ のうち、パターンに含まれない数も高速に求めることができる。 $0$ から考えて、長さ $4$ のパターンは $7$ つあるから残りの数は $[4*7, 30]$ である。このうち、最初の $2^1$ 個目までの数の $1$ ビット目は $0$ になっていて、残りの数が $1$ となっている。

パターンに含まれる数の和は、パターンごとの総和を考えると $1$ ビット目の場合、 $5,13,21,29,37,45,53$ となっていることがわかる。これは初項 $5$ で公差が $2^3$ 項数 $7$ の等差数列の和をとることで $O(1)$ で求めることができる。

パターンに含まれない数の和は初項 $30$ 公差 $1$ で末項 $30$ の等差数列の和を求めれば良い。

f:id:d_tutuz:20180929124603p:plain

上記の内容を一般化すると、

$n$ までの数のうち $k$ ビット目は・・・

パターンが $\displaystyle \frac{n+1}{2 * 2^k}$ 個
パターンに含まれる数の総和は初項が「初項 $2^k$ 公差 $1$ 項数 $k$ の等差数列の和」、公差が $2^{2*k+1}$ 項数 $\displaystyle \frac{n+1}{2 * 2^k}$ の等差数列の和（＝上の図でいうところのオレンジ背景の部分）
パターンに含まれない数の総和は初項 $\displaystyle \frac{n+1}{2 * 2^k} * (2 * 2^k) + 2^k$ 公差 $1$ 項数 $(n+1) \% (2 * 2^k) - 2^k$ の等差数列の和（＝上の図でいうところの水色背景の部分）

となっている。

       public void solve(int testNumber, InputReader in, PrintWriter out) {

            long n = in.nextLong();

            long ans = 0;
            for (long k = 1; k <= n; k <<= 1) {
                long sum = sum(k, 1, k);
                long len = (n+1) / (2*k);
                ans += sum(sum, k % MOD * (2 * k % MOD) % MOD, len);
                ans %= MOD;
                long to = (n+1) % (2*k) - k;
                if (to > 0) {
                    long from = (n+1) / (2*k) * (2*k) + k;
                    ans += sum(from, 1, to);
                    ans %= MOD;
                }
            }

            out.println(ans);

        }

        long sum(long a, long d, long n) {
            a %= MOD;
            d %= MOD;
            n %= MOD;
            return n * (2 * a % MOD + (n + MOD - 1) % MOD * d % MOD) % MOD * INV2 % MOD;
        }

ポイント

パターンごとにまとめて考える

類題

雑記

本番中は popcount(x) の数が同じものでまとめられれば、同じ popcount(x) の数はまとめて計算できるのでは・・・。と考えていたが、popcount(x) の数が同じものでまとめれることを高速に実施することは難しそうと判断して、解けないなぁ...と思っていた。

2018-09-25

ABC077-D：Small Multiple

グラフ

問題

正整数 K が与えられる。K の倍数の集合の中で桁和が最小になるとき、その桁和を求めよ。

考え方

任意の正整数は 1 からはじめて、

操作

ある数 t に +1 する
ある数 t に × 10 する

を繰り返し適応することで求められる。上記の操作をするとき +1 するときのみ桁和が +1 される。

K の倍数の集合は mod K でみたときに 0 になる数である。数を同一視するために mod K で考える。

1 からはじめて上記操作によって 0 (mod K) に遷移するときの最小のコストが求める解である。これは K 頂点のそれぞれから、コスト +1 で +1 の頂点に遷移する辺とコスト 0 で *10 (mod K) の頂点に遷移するグラフを考えると、頂点 1 から頂点 0 への最短経路を求めることと同一である。よってダイクストラ法で O(KlogK) で求めることができた。

Submission #3266978 - AtCoder Beginner Contest 077

ポイント

$K$ の倍数 $\Leftrightarrow$ $0 \equiv mod K$
数全体の集合で考える

類題

2018-09-24

Codeforces Round #512

解いた問題を振り返ります。

A.In Search of an Easy Problem

問題概要

Problem - A - Codeforces

0 または 1 である n 個の文字列が与えられる。 1 つでも 1 が存在する場合は "HARD" をそうでない場合は "EASY" を出力せよ。

考え方

問題概要の指定されたとおりに実装すればいいです。

Submission #43300583 - Codeforces

B.Vasya and Cornfield

問題概要

Problem - B - Codeforces

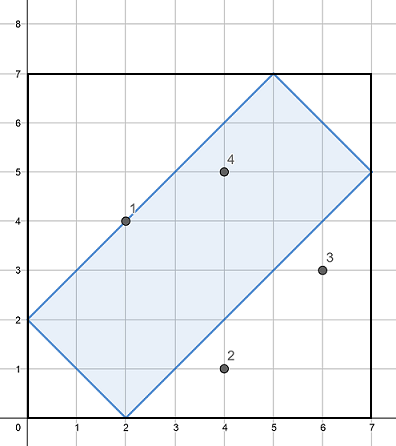「http://codeforces.com/predownloaded/d4/77/d4774c8e0335ef834f224f203b990e3154fc535a.png」より引用

$2$ 数, $n, d$ をもとに $(0, d), (d, 0), (n, n - d), (n - d, n)$ なる $x-y$ 平面上の $4$ 点が与えられる。その後 $m$ つの点が与えられる。点 $(x_i, y_i)$ が $4$ 点に内包されるかどうか確認せよ。内包される場合は "YES" そうでない場合は "NO" を出力する。

考え方

座標上の内包判定は直線の方程式を求めて、内包されるか判定すればよい。与えられた点から 4 つの直線の方程式を求めることができる。

$y \geq -x + d$
$y \leq -x + 2n - d$
$y \geq x - d$
$y \leq x + d$

$m$ つの点それぞれについて、この条件を満たすかどうか判定すればいい。

Submission #43365208 - Codeforces

ポイント

図形を数式で表現する

類題

C.Vasya and Golden Ticket

問題概要

Problem - C - Codeforces

長さ n の数列 a が与えられる。a を 2 つ以上のいくつかに分割して、それぞれの分割された区間の和が等しくなるようにしたい。そのような分割が存在する場合は "YES" をそうでない場合は "NO" を出力せよ。

考え方

まず数列 a が全て 0 の場合は可能であるから "YES" である。制約が小さいため分割されたときの区間の和を全探索することができる。

数列 a の和を sum としておく。区間の和 t は [1, sum-1] を全探索する。

まず sum が t で割り切れない場合はそのような分割はできないため、"NO"である。

そうでない場合は数列を順に参照していき、[i, j] が t になったタイミングで t を 0 でリセットして次の要素から調べる。同様に [j+1,k] の和も t になったタイミングで 0 にリセットする。そのようにして数列の要素を最後まで調べることができれば t で分割することが可能であることがわかるから "YES"。そうでない場合は [1, sum-1] なるいずれの t でも分割することはできないため "NO" となる。

Submission #43365918 - Codeforces

ポイント

全探索
コーナーケース(すべてが 0 の場合)に注意

雑記

すべてが 0 の場合に気づかなくて、スコアを溶かしてしまいました・・・

D.Vasya and Triangle

問題概要

Problem - D - Codeforces

$n, m, k$ が与えられる。格子点上の 3 点 $(x_1, y_1), (x_2, y_2), (x_3, y_3)$ を選択して $3$ 点で内包される三角形の面積が $\displaystyle \frac{nm}{k}$ に等しくできる場合は "YES" を出力して、そのような $3$ 点を出力せよ。そうでない場合は "NO" を出力せよ。

考え方

$1$ 点を $(0, 0)$ にとり、他の $2$ 点を $x, y$ 軸上の $(0, x), (y, 0)$ にとることにする。このときの三角形の面積は $\displaystyle \frac{xy}{2}$ である。これが $\displaystyle \frac{nm}{k}$ と一致すれば良い。

格子点上の三角形 (多角形) の面積はピックの定理より $\displaystyle \frac{1}{2}$ の倍数になる。よってまず $2nm$ が $k$ で割り切れない場合は "NO" である。

$n, m$ について $k$ との最大公約数で割り、既約分数にする。 $2nm$ は $k$ で割り切れるため、 $nm$ を $k$ との最大公約数で割って既約分数にしたとき $k$ は $1$ ( $mn$ が $k$ で割り切れる場合)または $2$ ( $mn$ が $k$ で割り切れず $k$ が $2$ の倍数になっている時)となっている。

$k$ が $1$ となっている場合 $n, m$ と $k$ のいずれかの最大公約数が $2$ 以上になっているため、割れた数について、分子分母を $2$ 倍することで $\displaystyle \frac{xy}{2}$ と合わせることができる。そのときの $n, m$ が $x, y$ となる。

$k$ が $2$ となっている場合は、すでに $\displaystyle \frac{xy}{2}$ の形になっているため、その時の $n, m$ を出力すればよい。

Submission #43367380 - Codeforces

ポイント

分数の形を揃える
ピックの定理

類題

2018-09-24

ABC110-D：Factorization

高校数学数え上げ

問題

正整数 $N, M$ が与えられる。 $a_1 * a_2 * ... * a_N = M$ となる a の数列が何通りあるか求めよ。

考え方

例として $2^3 * 3^2 * 5^2 = 1800, N = 4$ とする。

まずは $M$ を素因数分解をする。それぞれの因数ごとに独立して考えることができる。因数ごとのべき乗の数がポイントである。

$2^3$ を x x x x のような $4$ つのマスに配る配り方の場合の数を考える。左から $a, b, c, d$ ( $a, b, c, d$ は非負数)個あるような配り方を考えると、 $a + b + c + d = 4$ となるような $3$ つの $2$ を配る場合の数と同じである。

これは重複組合せで求めることができる。上の例であれば ${}_{4 + 3 - 1} \mathrm{C}_4$ で求めることができる。 $3$ の配り方、 $5$ の配り方も同様に ${}_{4 + 2 - 1} \mathrm{C}_4$ と ${}_{4 + 2 - 1} \mathrm{C}_4$ と求めることができ、解はそれぞれをかけ合わせればいい。

ポイント

因数ごとに独立して考えてよい
素因数分解して指数に着目する

類題

雑記

これも難しかった。各因数について独立して考えて良いという点に気づきませんでした・・・

2018-09-24

ABC110-C：String Transformation

問題

文字列 S, T が与えられる。S のうち、異なる 2 つの英小文字 c1, c2 を選んで swap させる。 0 回以上 swap させて文字列 S を T にすることができるかどうは判定せよ。

考え方

文字の変更先は一意に定まる。同じ文字からは同じ文字にしか変更できない。以下のような文字列は swap によって実現できない。

a b c
a a b

つまり $s_i = s_j$ であれば、 $t_i = t_j$ となる。逆に $s_i ≠ s_j$ であれば、 $t_i ≠ t_j$ となる。これを判定すればいい。

ポイント

全単射
文字列の swap

類題

雑記

これ難しい・・・

2018-09-21

COLOCON -Colopl programming contest 2018-：すぬけそだて――ごはん――

問題

https://beta.atcoder.jp/contests/colopl2018-qual/tasks/colopl2018_qual_c

[a, b] の数から 0 個以上の要素を選んで集合 S とする。集合 S に含まれる要素はそれぞれ互いに素である。このような集合 S は何通りあるか？

考え方

以下の 2 つ考えられる。

(i) [a, b] を全探索

最大 36 個の要素で全探索をすると 2³⁶ ≒ 7 * 10¹⁰ となる。ただし実は全探索する過程で、集合 S に含めることのできない要素については枝刈りされるので dfs で全探索することができる。

Submission #4144792 - COLOCON -Colopl programming contest 2018-

(ii) 素因数でビットDP

集合 S に [a, b] のある数 n を含めることができる場合は、n の素因数は集合 S の素因数には含まれない場合である。b - a <= 35 であるから、[a, b] は [1, 36] の中に含まれる素因数を取りうる。[1, 36] の中に含まれる素数は

{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31}

の 11 つである。よって、以下のような状態遷移を考えることができる。

dp[i][bit] := [a, b] の i 番目まで参照したときの素因数 {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31} の部分集合

とすると、

(A)bit に含まれる素因数と n に含まれる素因数に重なりがない場合
dp[i][bit] -> dp[i+1][bit + state] (state は n に含まれる素因数の集合)

(B)bit に含まれる素因数と n に含まれる素因数が重なる場合
dp[i][bit] -> dp[i+1][bit]

DP初期値は dp[0][0] = 1 として求めることができる。

       public void solve(int testNumber, InputReader in, PrintWriter out) {

            long a = in.nextLong(), b = in.nextLong();

            long[] prime = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31};
            long[][] dp = new long[37][1 << 11];
            dp[0][0] = 1;

            int n = (int)(b - a + 1);
            for (int i = 0; i < n; i++) {

                int sum = 0;
                for (int j = 0; j < 11; j++) {
                    if ((i + a) % prime[j] == 0) sum += 1 << j;
                }

                for (int bit = 0; bit < 1 << 11; bit++) {
                    if ((bit & sum) == 0) {
                        dp[i+1][bit + sum] += dp[i][bit];
                    }
                    dp[i+1][bit] += dp[i][bit];
                }
            }

            long ans = 0;
            for (int bit = 0; bit < 1 << 11; bit++) {
                ans += dp[n][bit];
            }

            out.println(ans);

        }

どこに着目して考察するべきだったか

極端な制約 $b - a \le 35$ に着目する。また偶数と互いに素になる数は奇数であること、購入した数の集合が増えると、互いに素になれる数の候補が小さくなっていくことから枝刈り全探索が自然に出てくる

典型ポイント

枝刈り全探索

類題

雑記

最初は 2 を素因数にもつ数の個数、3 を素因数にもつ数の個数、6 を素因数にもつ数の個数、その他の個数に分けて、うまいこと処理しようとしたが思ったより面倒で実装でもバグらせた。ちゃんと遷移を考えることが重要でした。